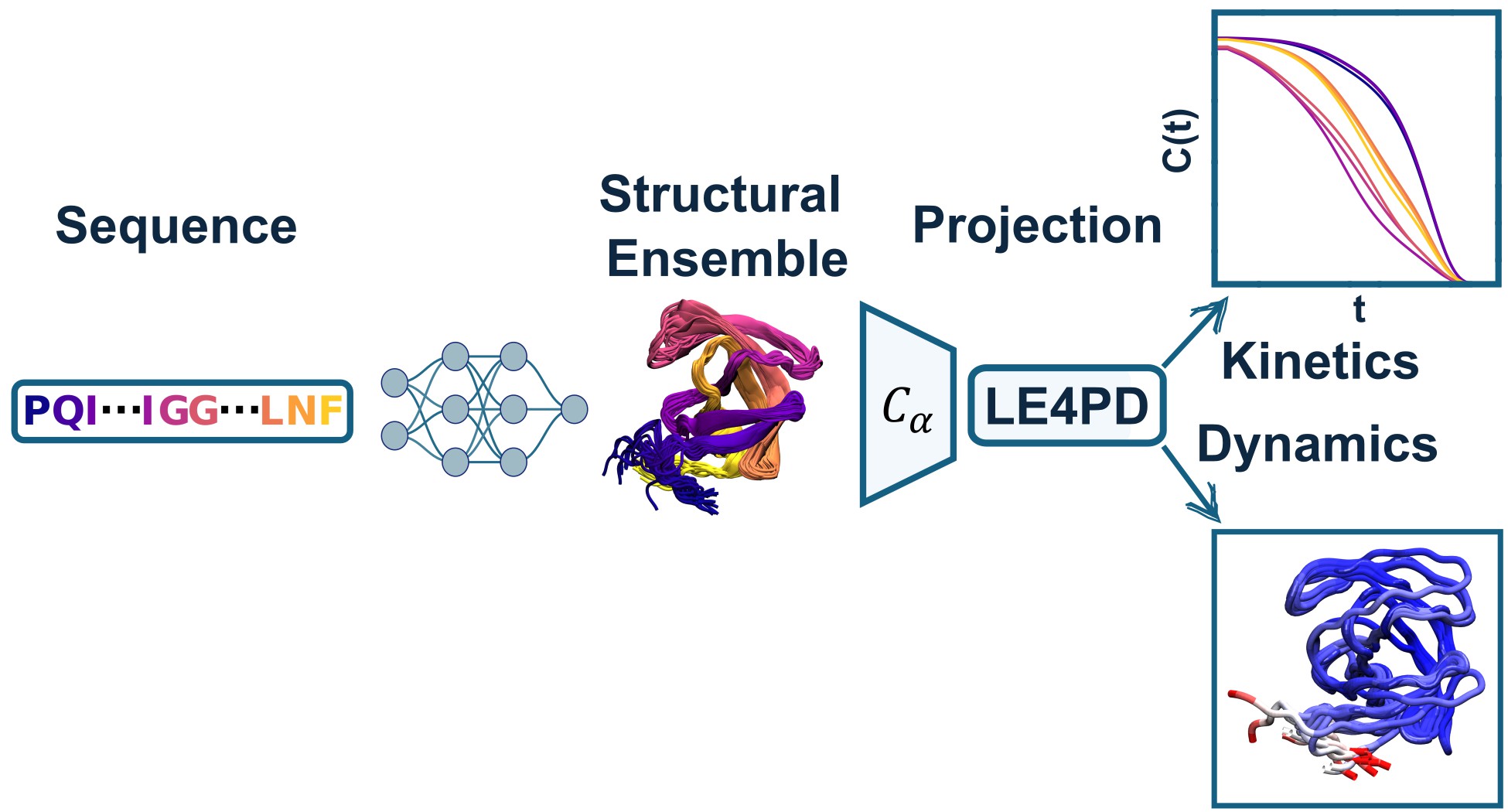
While, at least contemporarily, generative machine-learning approaches for creating conformational ensembles of proteins are becoming more and more popular,
they still lack critical information regarding the timescales (or kientics) of the motions encoded by the generated ensemble. To at least partially alleviate this
issue, we couple the output ensembles from a few contemporary machine learning architectures to a coarse-grained Langevin equation and
solve the equations of motion in the quasi-independent Langevin mode space, where each mode of motion possesses a characteristic relaxation timescale and fluctuation
profile along the primary sequence of the protein. We perform this analysis for six variants of the HIV-1 protease monomer and benchmark the results against microsecond
molecular dynamics simulations. We find that the relaxation timescales predicted from AlphaFold2 to be
inversely proportional to the multiple sequence alignment depth specified, and that, for the lowest depth tested (8 sequences), the relaxation timescales from
AlphaFold2 are comparable to those generated by microsecond simulations. We also find that the BioEmu architecture predicts similar relaxation timescales, but it
generates fewer "deepfake" structures (lying outside the span of the microsecond simulations).
